Dang Van method

The criterion was first presented in [DV73]. It started a branch of mesoscopic criteria, which found a continuation in the Papadopoulos and Morel criteria. The mesoscopic criteria have their common point in an assumption that not the apparent macroscopic quantities, but their mesoscopic counterpart related to the least homogenous agglomerates of grains should be checked for fatigue evaluation. Dang Van initiated the solution and presented a way of transforming the mesoscopic quantities towards macroscopic stresses. The solution in PragTic is related only towards fatigue limit, thus it can be written as:

where the critical plane is set by maximization of the left hand side of the equation. See the nomenclature section below for explanation of symbols. Since hydrostatic stress is independent from the cutting plane direction, the criterion can be seen both as MSSR method and MD method all in one. Variables in the criterion are set by maximization of the left hand side for cases of fully reversed torsion and tension. It can be derived that:

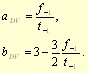
The Dang Van formula is widely used, although its predictive efficiency is reported as not very good [BPL03], [Del04], [FatLim Database]. The method is implemented in some of the commercial software (Fe-Safe, LMS.Virtual Lab Component Durability), thus it was included into the PragTic too.

Nomenclature:

Mark	Unit	PragTic variable	Meaning
	[MPa]		shear stress amplitude on an examined plane
	[MPa]	TENS-1, BEND-1	fatigue limit in fully reversed axial loading
	[MPa]		maximum value of hydrostatic stress during load history
	[MPa]	TORS-1	fatigue limit in fully reversed torsion

Methods & Options & Variables of Calculation – Edit

Decomposition

- Whole load path

Elasto-plasticity

- No – currently no option implemented

Solution option

- Searched planes <0~BS algorithm, 1~globe analogy, 2~random>

- Number of scanned planes

- Optimize <1~yes, 0~no>

- Only every x-th data-point taken from load history

- Evaluate envelope curve only <1~yes, 0~no>

Solution variable

- Minimum damage – this option is not active for this high-cycle fatigue method

Material parameters

E	[MPa]	tensile modulus
NU	[-]	Poisson’s ratio
TENS-1	[MPa]	fatigue limit in fully reversed push-pull (or plane bending)
TORS-1	[MPa]	fatigue limit in fully reversed torsion

Result detail variables

Damage fatigue index is computed, not the damage as a reciprocal value to number of cycles or repetitions

FDD1 NCX x-coordinate of the normal line vector of the critical plane

FDD2 NCY y-coordinate of the normal line vector of the critical plane

FDD3 NCZ z-coordinate of the normal line vector of the critical plane

FDD4 ALFA angle between the normal lines to the critical plane and to the free surface

This help file has been generated by the freeware version of HelpNDoc